Where expr, expr_1, ..., expr_n can be either
expressions, or Maxima or Lisp functions or operators, or a list with
the any of the forms: [discrete, [x1, ..., xn],
[y1, ..., yn]], [discrete, [[x1, y1],
..., [xn, ..., yn]] or [parametric, x_expr,
y_expr, t_range].
Displays a plot of one or more expressions as a function of one variable.
plot2d plots one expression expr or several expressions
[name_1, ..., name_n]. The expressions that are not
of the parametic or discrete types should all depend only on one
variable var and it will be mandatory the use of x_range to
name that variable and gives its minimum and maximum values, using the
syntax: [variable, min, max]. The plot will
show the horizontal axis bound by the values of min and max.
A expression to be plotted can also be given in the discrete or
parametric forms. Namely, as a list starting with the word "discrete"
or "parametric". The keyword discrete must be followed by two
lists of values, both with the same length, which are the horizontal and
vertical coordinates of a set of points; alternatively, the coordinates
of each point can be put into a list with two values, and all the
coordinates of the points should be inside another list. The keyword
parametric must be followed by two expressions x_expr and
y_expr, and a range of the form [param, min,
max]. The two expressions must depend only on the parameter
param, and the plot will show the path traced out by the point
with coordinates (x_expr, y_expr) as param increases
from min to max.
The range of the vertical axis is not mandatory. It is one more of the
options for the command, with the syntax: [y, min,
max]. If that option is used, the plot will show that entire
range, even if the expressions do not reach all that range. Otherwise,
if a vertical range is not specified by set_plot_option, the
boundaries of the vertical axis will be set up automatically.
All other options should also be lists, starting with the name of the option. The option xlabel can be used to give a label for the horizontal axis; if that option is not used, the horizontal axis will be labeled with the name of the variable specified in x_range, or with the expression x_expr in the case of just one parametric expression, or it will be left blank otherwise.
A label for the vertical axis can be given with the ylabel option. If there is only one expression to be plotted and the ylabel option was not used, the vertical axis will be labeled with that expression, unless it is too large, or with the expression y_expr if the expression is parametric, or with the text "discrete data" if the expression is discrete.
The options [logx] and [logy] do not need any
parameters. They will make the horizontal and vertical axes be
scaled logarithmically.
If there are several expressions to be plotted, a legend will be written to identiy each of the expressions. The labels that should be used in that legend can be given with the option legend. If that option is not used, Maxima will create labels from the expressions.
By default, the expressions are plotted as a set of line segments joining adjacent points within a set of points which is either given in the discrete form, or calculated automatically from the expression given, using an algorithm that automatically adapts the steps among points using as an initial estimate of the total number of points the value set with the nticks option. The option style can be used to make one of the expressions to be represented as a set of isolated points, or as points and line segments.
There are several global options stored in the list plot_options
which can be modified with the function set_plot_option; any of
those global options can be overriden with options given in the
plot2d command. There are also other options which are not part of
the global options array plot_options and which can be given only
as part of the plot2d command; those options are: logx,
logy, box, legend, xlabel, ylabel,
psfile and style.
A function to be plotted may be specified as the name of a Maxima or Lisp function or operator, a Maxima lambda expression, or a general Maxima expression. If specified as a name or a lambda expression, the function must be a function of one argument.
Examples:
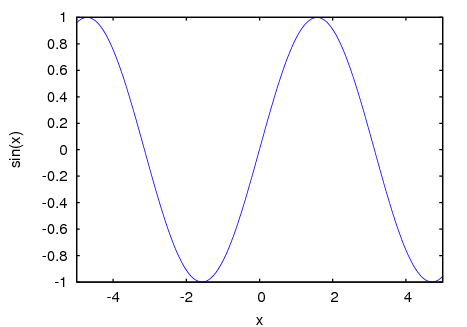
Plots of common functions.
(%i1) plot2d (sin(x), [x, -5, 5])$ (%i2) plot2d (sec(x), [x, -2, 2], [y, -20, 20], [nticks, 200])$
Plotting functions by name.
(%i3) F(x) := x^2 $ (%i4) :lisp (defun |$g| (x) (m* x x x)) $g (%i5) H(x) := if x < 0 then x^4 - 1 else 1 - x^5 $ (%i6) plot2d (F, [u, -1, 1])$ (%i7) plot2d ([F, G, H], [u, -1, 1], [y, -1.5, 1.5])$
We can plot a circle using a parametric plot with a parameter t. It is not necessary to give a range for the horizontal range, since the range of the parameter t determines the domain. However, since the graph's horizontal and vertical axes lengths are in the 4 to 3 proportion, we will use the xrange option to obtain the same scaling in both axes:
(%i8) plot2d ([parametric, cos(t), sin(t), [t,-%pi,%pi],
[nticks,80]], [x, -4/3, 4/3])$
If we repeat that plot with only 8 points and extending the range of the parameter to give two turns, we will obtain the plot of a star:
(%i9) plot2d ([parametric, cos(t), sin(t), [t, -%pi*2, %pi*2],
[nticks, 8]], [x, -2, 2], [y, -1.5, 1.5])$
Combination of an ordinary plot of a cubic polynomial with a parametric plot of a circle:
(%i10) plot2d ([x^3+2, [parametric, cos(t), sin(t), [t, -5, 5],
[nticks, 80]]], [x, -3, 3])$
Example of a logarithmic plot:
(%i11) plot2d (exp(3*s), [s, -2, 2], [logy])$
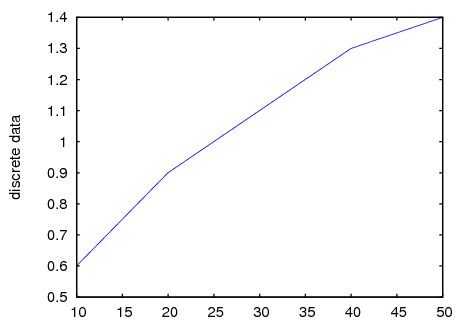
To show some examples of discrete plots, we will start by entering the coordinates of 5 points, in the two different ways that can be used:
(%i12) xx:[10, 20, 30, 40, 50]$ (%i13) yy:[.6, .9, 1.1, 1.3, 1.4]$ (%i14) xy:[[10,.6], [20,.9], [30,1.1], [40,1.3], [50,1.4]]$
To plot those data points, joined with line segments, we use:
(%i15) plot2d([discrete,xx,yy])$
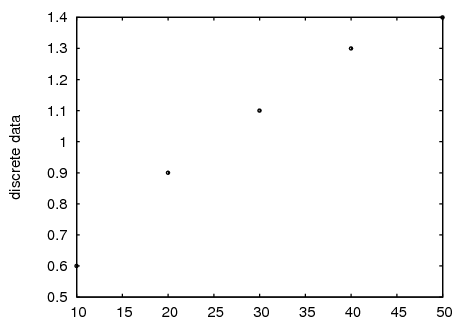
We will now show the plot with only points, and illustrating the use of the second way of giving the points coordinates:
(%i16) plot2d([discrete, xy], [style, points])$
The plot of the data points can be shown together with a plot of the theoretical function that predicts the data:
(%i17) plot2d([[discrete,xy], 2*%pi*sqrt(l/980)], [l,0,50],
[style, [points,5,2,6], [lines,1,1]],
[legend,"experiment","theory"],
[xlabel,"pendulum's length (cm)"], [ylabel,"period (s)"])$
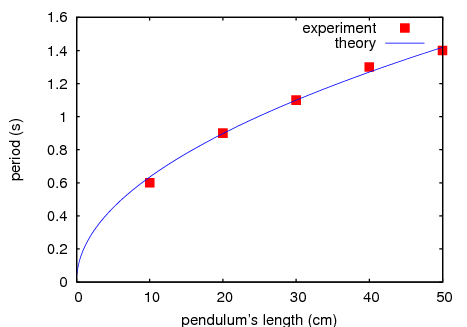
The meaning of the three numbers after the "points" style option are as follows; 5: radius of the points, 2: index of color used (red), 6: type of objects used (solid squares). The two numbers after the "lines" style option give the thickness of the line (1 point) and the color (1 corresponds to blue).
To save a plot of sin(x) to the file sin.ps, one can use:
(%i18) plot2d (sin(x), [x, 0, 2*%pi], [psfile, "sin.eps"])$
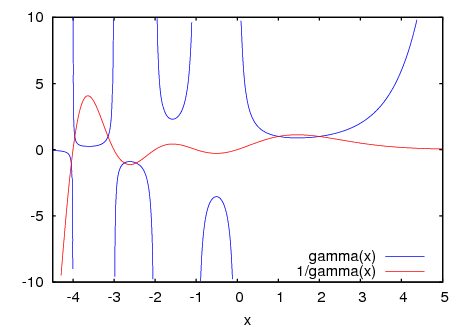
The next example uses the y option to chop off singularities and the gnuplot_preamble option to put the key at the bottom of the plot instead of the top.
(%i19) plot2d ([gamma(x), 1/gamma(x)], [x, -4.5, 5], [y, -10, 10],
[gnuplot_preamble, "set key bottom"])$
We can also use a gnuplot_preamble to produce fancy x-axis
labels. (Note that the gnuplot_preamble string must be entered
without any line breaks.)
(%i20) my_preamble: "set xtics ('-2pi' -6.283, \
'-3pi/2' -4.712, '-pi' -3.1415, '-pi/2' -1.5708, '0' 0, \
'pi/2' 1.5708, 'pi' 3.1415,'3pi/2' 4.712, '2pi' 6.283)"$
(%i21) plot2d([cos(x), sin(x), tan(x), cot(x)],
[x, -2*%pi, 2.1*%pi], [y, -2, 2], [axes, x]
[gnuplot_preamble, my_preamble]);

This example uses a gnuplot_preamble to produce fancy x-axis
labels, and produces PostScript output that takes advantage of the
advanced text formatting available in gnuplot. (Note that the
gnuplot_preamble string must be entered without any line breaks.)
(%i22) my_preamble: "set xtics ('-2{/Symbol p}' \
-6.283, '-3{/Symbol p}/2' -4.712, '-{/Symbol p}' -3.1415, \
'-{/Symbol p}/2' -1.5708, '0' 0,'{/Symbol p}/2' 1.5708, \
'{/Symbol p}' 3.1415,'3{/Symbol p}/2' 4.712, '2{/Symbol p}' \
6.283)"$
(%i23) plot2d ([cos(x), sin(x), tan(x)], [x, -2*%pi, 2*%pi],
[y, -2, 2], [gnuplot_preamble, my_preamble],
[psfile, "trig.eps"]);
See also plot_options, which describes plotting options.
@ref{Category: Plotting}